I have spent the last couple of years refining and deepening my understanding of mathematics and how children develop their own understanding of numbers, shapes, and concepts.There are number of games that you can play with your child to help support these skills.
I have shown a few below that we use in class during game day (Fridays), but here are some others you can check out:
Here are some we play at school that would also be great to play at home:
- Connect 4
- Checkers
- Chess
- Cribbage
- War (and its variations such as two card greatest/least sum (addition) or two card greatest/least difference (subtraction)
- Othello
- Go
- Dominoes
WCSU Math Coach Blog
We are starting to use a new math program this year called Ready Math. You can learn more about it below.
Ready Math
We use a number of manipulatives to help children understand the numbers we are asking them to think about and work with. The main concrete material we use is called a Cuisenaire Rod. These are colored rods that represent a number of units, from one to as large as you want to go. In first grade, we are looking at numbers roughly from 1-200.
Here is a sample video that shows some of what we do with the Cuisenaire Rods:
Addition Using Cuisenaire Rods
Counting
The oral language of numbers is critical to the understanding of them. Counting is often one of the first steps on this journey. In first grade math the expectation is for kids to be fluid counters from 0-120 forwards and backwards by 1's and 10's and also be able to count by tens from any number (4, 14, 24, for example). The goal is for students to be familiar with many counting patterns. We also use this understanding to help us use math tools like number lines and number charts.
Decomposition and Recomposition
It is really important for children to see numbers made of other numbers. We use many tools to help us do this. Children love dot cluster cards. They help children use their "mind's eye" to see numbers in many different ways. Students love seeing the different ways that their friends see numbers. Here's an example:
On this card, some students may see 4+4+1=9. They could see the lines of four spades on the sides or the clusters of four spades on the top and bottom. Others may see 5+2+2. You never know what they will see!
A Pictorial Tour Of How We Use Cuisenaire Rods
Here is a picture of a single unit (1)
We then can apply this concept to other numbers, such as the number 4. You can see how the number 4 is made up of four units. We do not want children to count 1,2,3,4, but rather to see the number 4 as representing four units. This helps them see that numbers can then be broken up into parts later on.
When we look at a number, say 7, we want children to see the facts that make seven in a systematic way. Therefore, seven should be seen as 7+0, 6+1, 5+2, etc. You can see the "staircase" that makes up any number. By seeing number facts in this kind of systematic way, they learn their facts quicker and with the understanding that numbers are made up of other numbers and can be put together and taken apart.
When students become comfortable with the parts of numbers, we can extend this to a problem, say 8+4.
We know that 8+2=10 (See progression below) and because we can break up 4 into 2+2, we know that 8+2+2=12.
It may appear complicated, but this is exactly the way in which we need to have students looking at and using numbers,
The Progression of Math Addition Skills:
There is so much to learn about math in first grade! The great part about this is that they are eager to learn about the mystery of numbers and unlocking the magic around them. When they start to feel in control of how numbers work, and how they work for them, it is a powerful time.
Additional Resources
http://www.math-aids.com/
http://www.homeschoolmath.net/
http://www.worksheetworks.com/
http://www.commoncoresheets.com/
https://media.pearsoncmg.com/curriculum/math/Investigations3/gamecenter/english/index.html#/Grade:1/
Here are some we play at school that would also be great to play at home:
- Connect 4
- Checkers
- Chess
- Cribbage
- War (and its variations such as two card greatest/least sum (addition) or two card greatest/least difference (subtraction)
- Othello
- Go
- Dominoes
WCSU Math Coach Blog
We are starting to use a new math program this year called Ready Math. You can learn more about it below.
Ready Math
We use a number of manipulatives to help children understand the numbers we are asking them to think about and work with. The main concrete material we use is called a Cuisenaire Rod. These are colored rods that represent a number of units, from one to as large as you want to go. In first grade, we are looking at numbers roughly from 1-200.
Here is a sample video that shows some of what we do with the Cuisenaire Rods:
Addition Using Cuisenaire Rods
Counting
The oral language of numbers is critical to the understanding of them. Counting is often one of the first steps on this journey. In first grade math the expectation is for kids to be fluid counters from 0-120 forwards and backwards by 1's and 10's and also be able to count by tens from any number (4, 14, 24, for example). The goal is for students to be familiar with many counting patterns. We also use this understanding to help us use math tools like number lines and number charts.
Decomposition and Recomposition
It is really important for children to see numbers made of other numbers. We use many tools to help us do this. Children love dot cluster cards. They help children use their "mind's eye" to see numbers in many different ways. Students love seeing the different ways that their friends see numbers. Here's an example:
On this card, some students may see 4+4+1=9. They could see the lines of four spades on the sides or the clusters of four spades on the top and bottom. Others may see 5+2+2. You never know what they will see!
A Pictorial Tour Of How We Use Cuisenaire Rods
Here is a picture of a single unit (1)
We then can apply this concept to other numbers, such as the number 4. You can see how the number 4 is made up of four units. We do not want children to count 1,2,3,4, but rather to see the number 4 as representing four units. This helps them see that numbers can then be broken up into parts later on.
When we look at a number, say 7, we want children to see the facts that make seven in a systematic way. Therefore, seven should be seen as 7+0, 6+1, 5+2, etc. You can see the "staircase" that makes up any number. By seeing number facts in this kind of systematic way, they learn their facts quicker and with the understanding that numbers are made up of other numbers and can be put together and taken apart.
When students become comfortable with the parts of numbers, we can extend this to a problem, say 8+4.
We know that 8+2=10 (See progression below) and because we can break up 4 into 2+2, we know that 8+2+2=12.
It may appear complicated, but this is exactly the way in which we need to have students looking at and using numbers,
The Progression of Math Addition Skills:
1.
Number Line
Students should be able to rote
count forward to at least 120. They should be able to
identify and name the
numbers when asked.
2.
Number+1 = 1+Number
The order of an addition problem
does not affect the answer.
3.
N+1
Students should be able to
identify the number after a number fluently
4.
Make 10
Students need to know
their combinations to make 10 both ways (ie. 1+9 and 9+1)
5.
N+10
Students need to be able to be given any number from
0-110 and be able to add ten to it (10+N and N+10)
6.
N+9
The strategy to find these answers is (N+10)-1. This
is the most efficient and preferred strategy we want students to be using.
7.
Doubles
Students need to know their
doubles from 1-10 up to 20.
8.
Doubles +1
This is the most efficient and
preferred strategy for solving problems like 6+7, etc
9.
N + (N-2)
This is the concept to solve
addition problems where the numbers are two apart. The idea is for them to
recognize that 7+5 is the double in between (6+6).
10.
N+2, 2+N
This is when students are able
to add two to a number (skipping a number)
11.
Near Tens
Students will be able to add
problems like 8+3, 3+6, and 4+7
12.
The Remaining Facts
8+4, 4+8, 8+5, 5+8. Students should
find their own way to learn these facts.
Place Value
We also need students to understand place value. That is, numbers in first grade can be made of hundreds, tens, and ones. We want students to be seeing numbers, made of parts. That way, children can eventually see in their heads the number 55. They know that 55 is made of 5 tens and 5 ones. If I ask them to add twelve to this number, they know they just need to add 1 ten and 2 ones. I can jump ten to 65 and then add two to get 67.
Here are some examples:
We also need students to understand place value. That is, numbers in first grade can be made of hundreds, tens, and ones. We want students to be seeing numbers, made of parts. That way, children can eventually see in their heads the number 55. They know that 55 is made of 5 tens and 5 ones. If I ask them to add twelve to this number, they know they just need to add 1 ten and 2 ones. I can jump ten to 65 and then add two to get 67.
Here are some examples:
5
(5 ones)
15
(1 ten and 5 ones)
55
(5 tens and 5 ones)
105
(1 hundred, 0 tens, 5 ones)
125
(1 hundred, 2 tens, 5 ones)
Using The Number Line To Solve Problems
Students need to know where numbers are on a continuum (number line). There is an order to them and that by knowing this order, we can figure out problems. In the beginning, we will practice using a full number line with students jumping one number at a time. As they become more fluent with their number knowledge, we move toward an open number line. Here are how they look and differ:
A beginning number line and its use:
Two frogs were in the pond. Four more came. How many are there now?
Open number line and its use (more advanced):
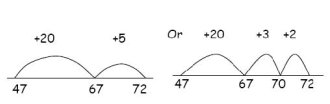
A sunflower is 47 cm tall. It grows another 25cm. How tall is it?
Additional Resources
http://www.math-aids.com/
http://www.homeschoolmath.net/
http://www.worksheetworks.com/
http://www.commoncoresheets.com/
https://media.pearsoncmg.com/curriculum/math/Investigations3/gamecenter/english/index.html#/Grade:1/
Cool- Great way ton engage a real math mind! There was a recent TED talk that showed that younger kids are not so interested in achieving the "right" solution to a puzzle , rather finding many different possible solutions. Approaching math in this way keeps that inquiry brain open!
ReplyDelete